Marked empirical process test statistic for a given GLM

This class inherits from TestStatistic and implements a function to calculate the test statistic (and x-y-values that can be used to plot the underlying process).

The process underlying the test statistic is given in Dikta & Scheer (2021) doi:10.1007/978-3-030-73480-0 and defined by $$\bar{R}^1_n(u) = \frac{1}{\sqrt{n}} \sum_{i=1}^n \left( Y_i - m(X_i, \hat{\beta}_n) \right) I_{\{\hat{\beta}_n X_i \le u\}}, \quad -\infty \le u \le \infty.$$

Super class

gofreg::TestStatistic -> MEP

Methods

Public methods

• MEP$calc_stat()

• MEP$clone()

Inherited methods

• gofreg::TestStatistic$geom_ts_proc()
• gofreg::TestStatistic$get_plot_xy()
• gofreg::TestStatistic$get_value()
• gofreg::TestStatistic$plot()
• gofreg::TestStatistic$print()

---

Method calc_stat()

Calculate the value of the test statistic for given data and a model to test for.

Usage

MEP$calc_stat(data, model)

Arguments

data

data.frame() with columns x and y containing the data

model

ParamRegrModel to test for

Returns

The modified object (self), allowing for method chaining.

---

Method clone()

The objects of this class are cloneable with this method.

Usage

MEP$clone(deep = FALSE)

Arguments

deep

Whether to make a deep clone.

Examples

# Create an example dataset
n <- 100
x <- cbind(runif(n), rbinom(n, 1, 0.5))
model <- NormalGLM$new()
y <- model$sample_yx(x, params=list(beta=c(2,3), sd=1))
data <- dplyr::tibble(x = x, y = y)

# Fit the correct model
model$fit(data, params_init=list(beta=c(1,1), sd=3), inplace = TRUE)

# Print value of test statistic and plot corresponding process
ts <- MEP$new()
ts$calc_stat(data, model)
print(ts)
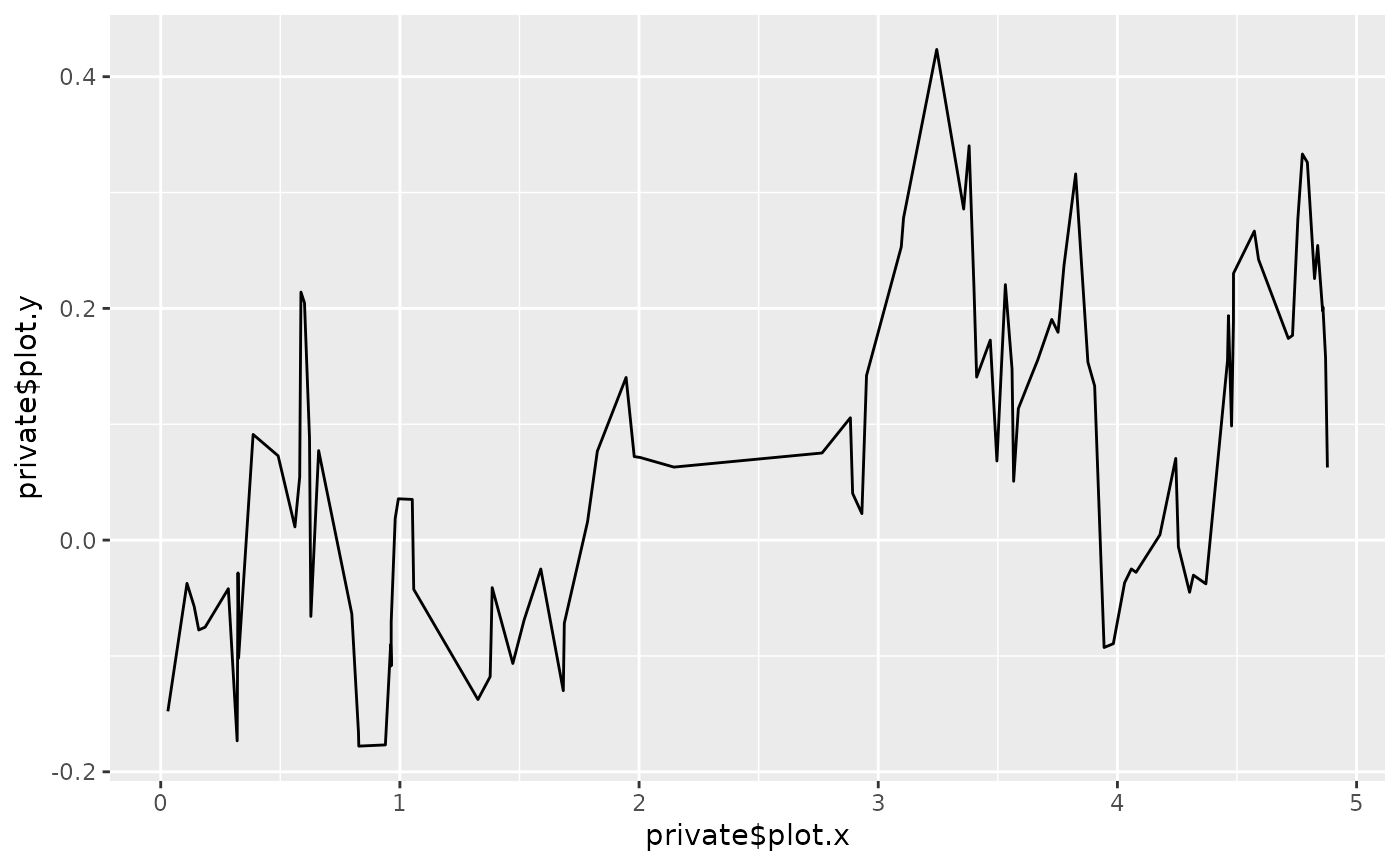
#> Test statistic with value 0.4235113
plot(ts)


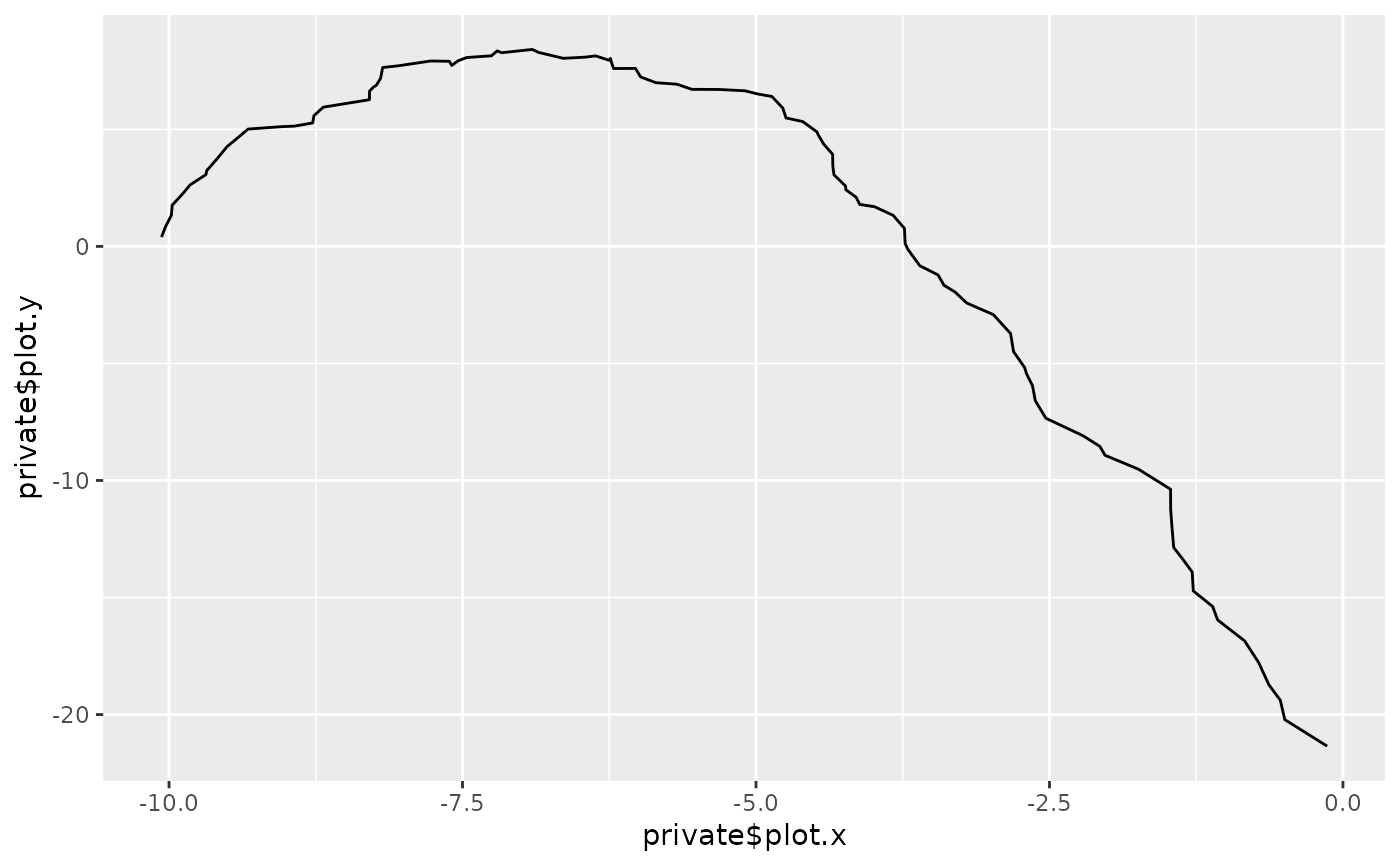
# Fit a wrong model
model2 <- NormalGLM$new(linkinv = function(u) {u+10})
model2$fit(data, params_init=list(beta=c(1,1), sd=3), inplace = TRUE)

# Print value of test statistic and plot corresponding process
ts2 <- MEP$new()
ts2$calc_stat(data, model2)
print(ts2)
#> Test statistic with value 21.34835
plot(ts2)