Generalized linear model with normal distribution

This class represents a generalized linear model with normal distribution. It inherits from GLM and implements its functions that, for example, evaluate the conditional density and distribution functions.

Super classes

gofreg::ParamRegrModel -> gofreg::GLM -> NormalGLM

Methods

Public methods

• NormalGLM$fit()

• NormalGLM$f_yx()

• NormalGLM$F_yx()

• NormalGLM$F1_yx()

• NormalGLM$sample_yx()

• NormalGLM$clone()

Inherited methods

• gofreg::ParamRegrModel$get_params()
• gofreg::ParamRegrModel$set_params()
• gofreg::GLM$initialize()
• gofreg::GLM$mean_yx()

---

Method fit()

Calculates the maximum likelihood estimator for the model parameters based on given data.

Usage

NormalGLM$fit(
  data,
  params_init = private$params,
  loglik = loglik_xy,
  inplace = FALSE
)

Arguments

data

tibble containing the data to fit the model to

params_init

initial value of the model parameters to use for the optimization (defaults to the fitted parameter values)

loglik

function(data, model, params) defaults to loglik_xy()

inplace

logical; if TRUE, default model parameters are set accordingly and parameter estimator is not returned

Returns

MLE of the model parameters for the given data, same shape as params_init

---

Method f_yx()

Evaluates the conditional density function.

Usage

NormalGLM$f_yx(t, x, params = private$params)

Arguments

t

value(s) at which the conditional density shall be evaluated

x

matrix of covariates, each row representing one sample

params

model parameters to use (list() with tags beta and sd), defaults to the fitted parameter values

Returns

value(s) of the conditional density function, same shape as t

---

Method F_yx()

Evaluates the conditional distribution function.

Usage

NormalGLM$F_yx(t, x, params = private$params)

Arguments

t

value(s) at which the conditional distribution shall be evaluated

x

matrix of covariates, each row representing one sample

params

model parameters to use (list() with tags beta and sd), defaults to the fitted parameter values

Returns

value(s) of the conditional distribution function, same shape as t

---

Method F1_yx()

Evaluates the conditional quantile function.

Usage

NormalGLM$F1_yx(t, x, params = private$params)

Arguments

t

value(s) at which the conditional quantile function shall be evaluated

x

matrix of covariates, each row representing one sample

params

model parameters to use (list() with tags beta and sd), defaults to the fitted parameter values

Returns

value(s) of the conditional quantile function, same shape as t

---

Method sample_yx()

Generates a new sample of response variables with the same conditional distribution.

Usage

NormalGLM$sample_yx(x, params = private$params)

Arguments

x

matrix of covariates, each row representing one sample

params

model parameters to use (list() with tags beta and sd), defaults to the fitted parameter values

Returns

vector of sampled response variables, same length as nrow(x)

---

Method clone()

The objects of this class are cloneable with this method.

Usage

NormalGLM$clone(deep = FALSE)

Arguments

deep

Whether to make a deep clone.

Examples

# Use the built-in cars dataset
x <- datasets::cars$speed
y <- datasets::cars$dist
data <- dplyr::tibble(x=x, y=y)

# Create an instance of a NormalGLM
model <- NormalGLM$new()

# Fit a Normal GLM to the cars dataset
model$fit(data, params_init = list(beta=3, sd=2), inplace=TRUE)
params_opt <- model$get_params()

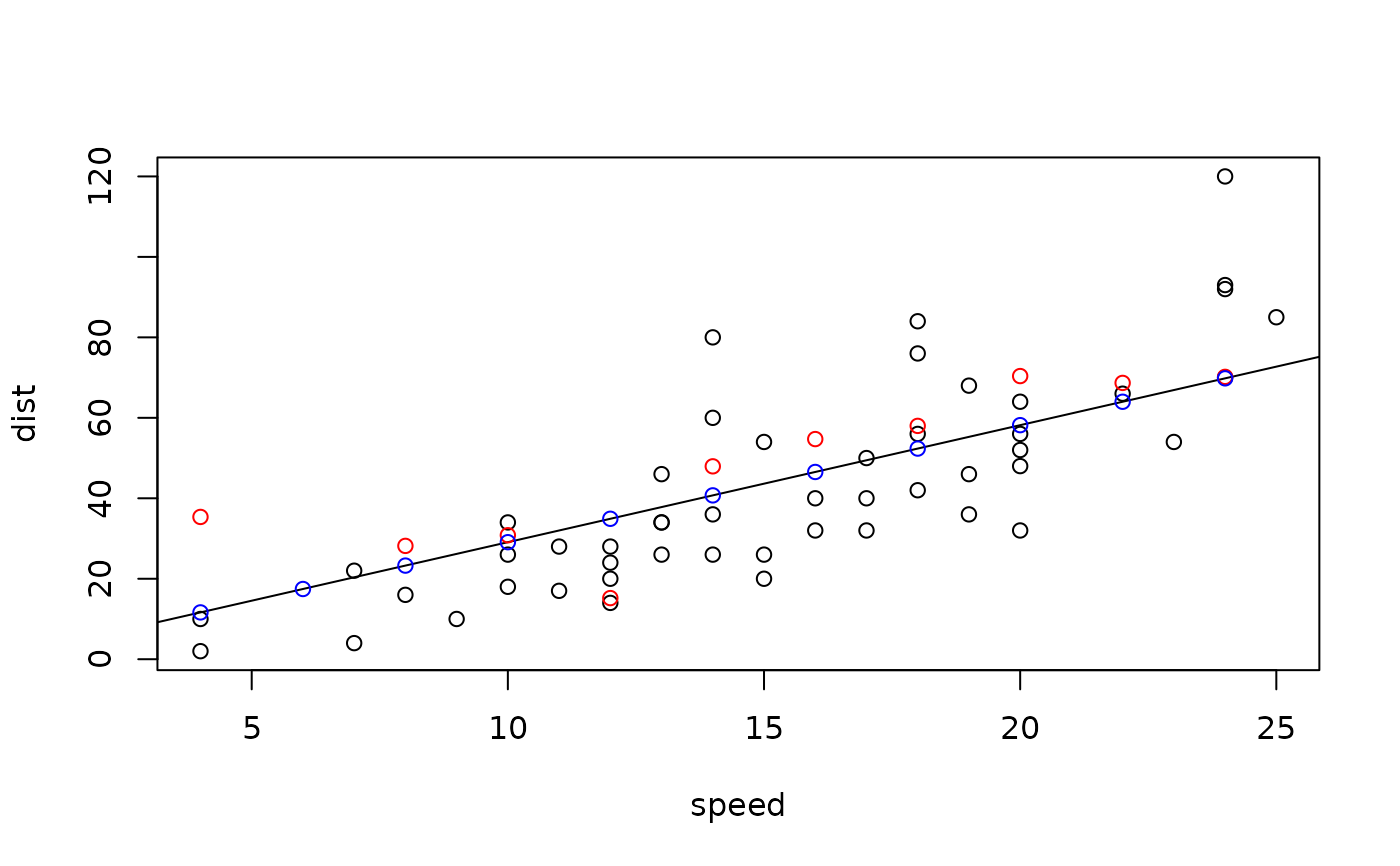
# Plot the resulting regression function
plot(datasets::cars)
abline(a = 0, b = params_opt$beta)

# Generate a sample for y for given x following the same distribution
x.new <- seq(min(x), max(x), by=2)
y.smpl <- model$sample_yx(x.new)
points(x.new, y.smpl, col="red")

# Evaluate the conditional density, distribution, quantile and regression
# function at given values
model$f_yx(y.smpl, x.new)
#>  [1] 0.008360204 0.007838506 0.023665601 0.024645091 0.011708252 0.022415827
#>  [7] 0.021786365 0.023313391 0.018595291 0.023760691 0.024781343
model$F_yx(y.smpl, x.new)
#>  [1] 0.92980773 0.06457848 0.61958855 0.54279090 0.11032669 0.67311101
#>  [7] 0.69429821 0.63691044 0.77583846 0.61444708 0.50911886
model$F1_yx(y.smpl, x.new)
#> Warning: NaNs produced
#>  [1] NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
y.pred <- model$mean_yx(x.new)
points(x.new, y.pred, col="blue")